Задания

 

          Задания  

 

 

 

 

Задание №1.

Существует легенда, что в старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции (синус на косинус), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента п/2+ а или п + а. Какой ответ получал математик, если лошадь кивала головой вдоль оси ОУ, а какой - если вдоль оси ОХ. Как называется это правило? (0,5б.) Сформулируйте его. (1,5б.)

С помощью сервиса mindmeister (формулы вставлять в виде рисунка) cоставьте карту знаний на тему "Формулы приведения" (5б.)

Критерии оценивания задания

Ответ к заданию №1

 

 

Задание №2.

Важный вклад в развитие тригонометрии были внесены математиками этой страны в период V-XII в.в. н.э. Им были известны соотношения, которые в современных обозначениях пишутся так: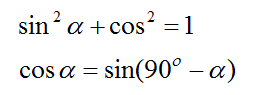 

Найдите эту страну на виртуальной карте, сделайте скриншот и отправьте на электронную почту учителя (3б.)

Критерии оценивания задания

Ответ к заданию №2

 

 

Задание №3.

1) Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 

Как известно, тригонометрия широко использовалась в древней астрономии. А для чего именно? (1б.)
Как назывался древнейший астрономический инструмент, позволяющий по наименьшей длине его тени (в полдень) определить угловую высоту солнца? Ответ найдите в облаке тегов. (2б.)

Что также позволяет определить этот инструмент? (1б.)

2) Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями. Впервые в IV-V веках появился специальный термин для этой функции в трудах по астрономии великого индийского учёного, именем которого назван первый индийский спутник Земли. Что это за ученый и о какой тригонометрической функции идет речь? (2б.)

3) Используя сервисы:

• Dipity - позволяет создать временную шкалу, вставлять в неё даты и их описание
• Timerime - позволяет создать временную шкалу, добавлять в неё изображения и видео
• Historama - представлены готовые ленты врмени 
• MyHistro

создайте ленту времени "История развития тригонометрических функций", которая должна собержать 10-12 дат, к каждой дате добавьте изображение (5б.)

Критерии оценивания задания

 

 

Задание №4.

1) Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции. Какой функции? С помощью сервиса y(x).ru постройте график этой функции. Скачайте изображение и отправьте на электронную почту учителя. (2б.)

2) Оказывается, очень многие явления в жизни можно объяснить с помощью синусоиды. Почему летом жарче, чем зимой? Почему для работы трамвая нужен постоянный ток? Почему в пустынях видны миражи? Почему после дождя светит радуга? Найдите ответы на эти вопросы. Ответ представьте в виде презентации (5б.)

Критерии оценивания задания

Ответ к заданию №4